A1-2 图像分类-kNN算法

课程《Deep Learning for Computer Vision》的作业1-2部分。

基本原理

kNN(k-nearest neighbor)是一种基本的分类方法，是一种监督学习方法。该算法需要带有标签的训练集，对于每一组测试数据，在训练集中寻找与其距离最近的$K$个元素，在分类问题中，这$K$个元素中出现次数最多的标签即为测试数据的标签。

距离可以有不同的度量方法，不同度量方法得到的结果也不同。对于图像数据，它可以用张量表示，通常有曼哈顿距离和欧几里得距离两种度量方法。若$I^p$为张量对应位置的元素，$d_1,d_2$分别为曼哈顿距离，欧几里得距离，则

$$d_1(I_1,I_2)=\sum_p |I_1^p-I_2^p|$$ $$d_2(I_1,I_2)=\sqrt{\sum_p(I_1^p-I_2^p)^2}$$

训练时间复杂度：由于该算法的训练过程只是把数据集保存起来，所以训练复杂度为$O(1)$
测试时间复杂度：对于每一个测试数据，我们要遍历训练集，计算它们之间的距离，所以测试复杂度为$O(N)$

可以看出，该算法训练很快，但实际预测的时候比较慢，这不是我们希望的结果，训练慢一些可以忍受，但实际预测很慢是一个很大的缺陷。

直观理解

假设我们要分类的图像只由两个像素组成，它可以表示为平面直角坐标系中的一个点。平面上不同颜色的区域代表不同的标签，横纵坐标分别表示其两个像素。

当$K$取不同的值时，分类情况不同，如下图

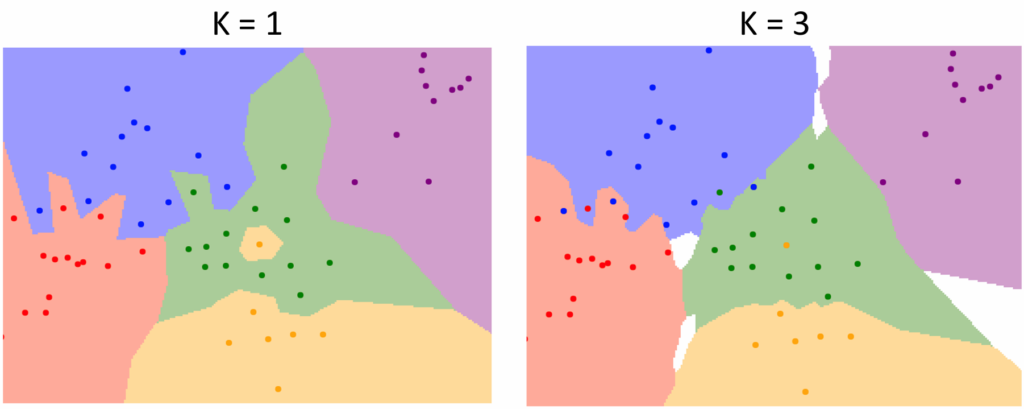
可以看出，$K=1$时不同颜色之间的交界非常曲折，而且还有黄色小区域被包含在绿色区域中的情况，会影响该区域周围点的判断；而$K=3$时分界线更为平滑，但此时不同类之间会出现空位。

当使用的距离定义不同时，分类情况不同，如下图

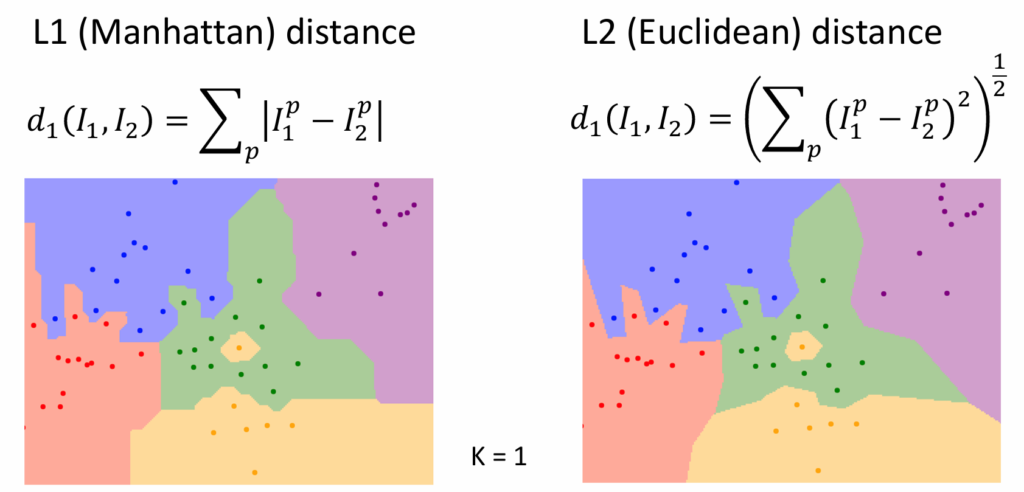
可以看出，当使用曼哈顿距离时，分界线的走向只能是固定角度，而使用欧几里得算法时，分界线的走向可以是任意的。

hyperparameters

从上面我们可以知道，当距离的度量方法或$K$不同时，分类的结果会不同，而这些值不是从训练中得到的，而是在开始之前我们人为设定的，它们会影响分类的结果，被称为hyperparameters，找到适当的值，对于算法的效果可以有显著影响。

参数调整

所以我们需要找到适当的方法来确定hyperparameter的值，基本思路是取那些能让训练结果最好的值。

例如，我们要确定$K$的值，首先，我们不能直接在所有数据上观察结果，因为那样会得到$K=1$，与自己重合准确率永远为100%，用训练集训练，测试集观察结果也是不恰当的，因为测试数据会污染原有的训练结果，无法预知其在新数据上的表现。更好的方法是，把所有数据分为训练集、验证集和测试集。通过验证集的结果取值，只在最后一步使用测试集测试结果，这样我们可以得知其在新数据上的表现。

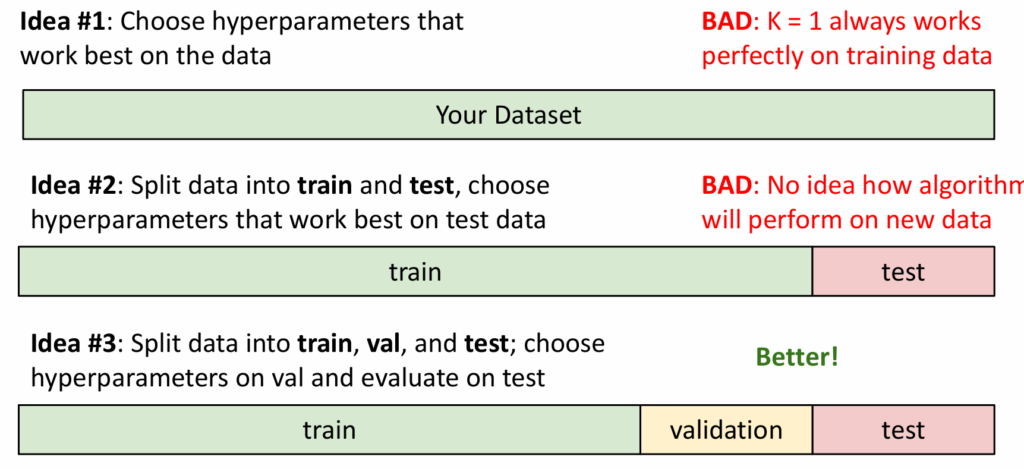
我们也可以把数据分成小块，使用多个验证集。

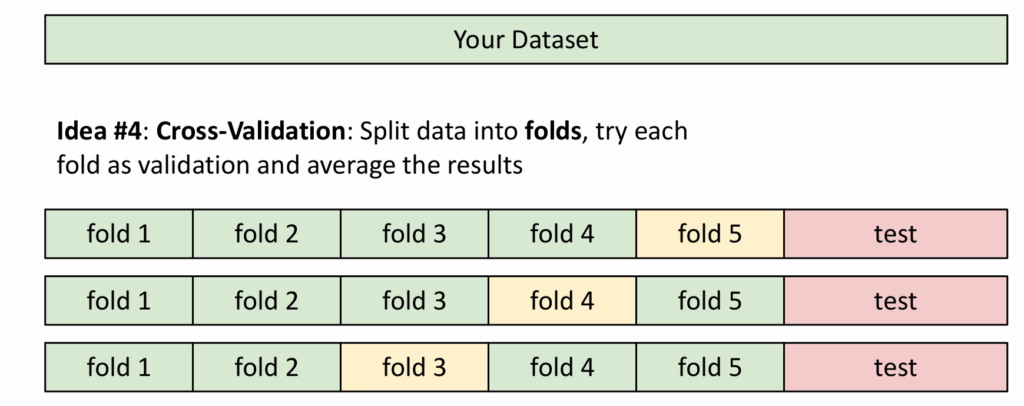
例如，对于每一个k，计算出平均准确度后，得到类似的图：

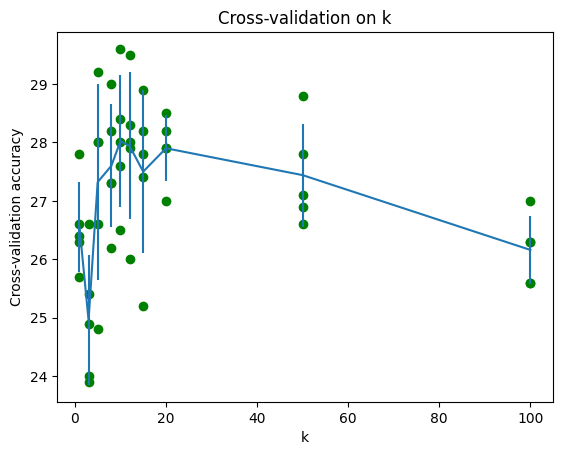
根据数据选出最合适的k值。

缺陷

• 测试时速度很慢
• 仅使用距离度量不能准确把握图像特征，如只对图像做一些简单的旋转，就可能大幅改变原图像的像素值

该算法在有些时候并不能得到很好的结果，但若把距离度量改成提取并比较图像的特征向量的方式，我们可以得到很好的结果。

A2 线性分类器（Linear Classifier）

参考资料：CS231n Convolutional Neural Networks for Visual Recognition

通过一个线性函数将输入映射到类别，即最终会得到每一个类别的“得分”。对于特征向量$\mathbf{x}=[x_1,x_2,…,x_n]$，决策函数为$$f(\mathbf{x})=\mathbf{w}^T\mathbf{x}+b$$
$\mathbf{w}$是权重向量，$b$是偏置量，训练一个分类器的过程，实际上就是通过特定算法找到合适的$\mathbf{w}$和$\mathbf{b}$。

SVM（支持向量机）

支持向量机算法的思想是要找到一个“超平面”，分开不同的类别。“超平面”实际上就是$\mathbf{w}^T\mathbf{x}+\mathbf{b}=0$，若输入向量是二维的，那它实际上就是一条直线，即在两类数据时间画一条直线，尽可能把它们分开并且直线到两类数据的距离都要尽量远。

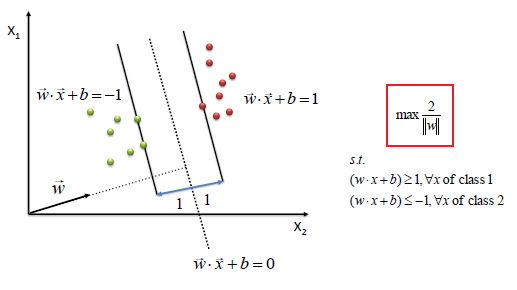
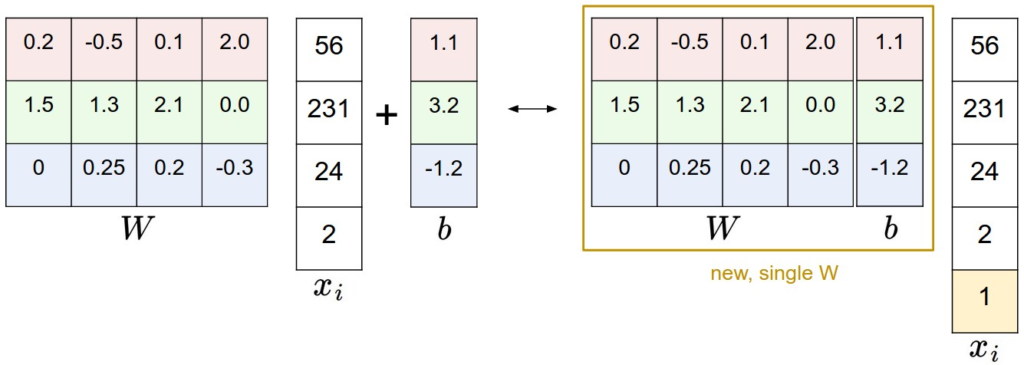
Bias Trick

可以把$\mathbf{b}$整合进$\mathbf{w}$中，只需在输入向量$\mathbf{x}$最后加上值等于1的一维即可达到与原来相同的效果

损失函数（Loss Function）

SVM使用Hinge Loss，对于第$i$组数据，计算表达式为$$L_i=\sum_{j\neq y_i}max(0, s_j – s_{y_i} + \Delta)$$
$y_i$为该组的正确类别，$j$为类别，$s$为得分，$\Delta$为安全边界，是一个hyperparameter
从上面的表达式我们可以看出，只有当$s_{y_i} – s_j < \Delta$时，才会累加loss，也就是，我们希望正确类别的得分要比其他类别的得分至少高出$\Delta$。

正则化（Regularization）

如果我们只是用上面的损失函数进行训练，机器为了尽可能减小loss，可能会导致某些权重非常大，这样训练出来的模型虽然在训练集上有很好的效果，但在验证集和测试集上效果会很差，这被称为过拟合（overfit）。

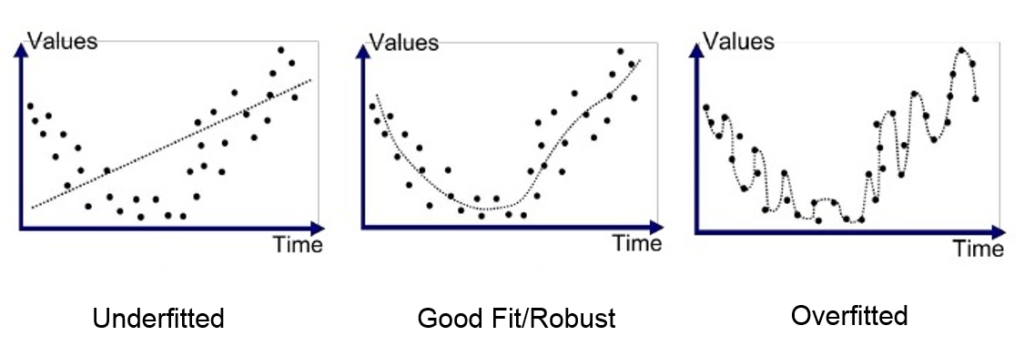
为了避免过拟合，我们可以在loss函数中增加一个量，用来限制模型无限拟合训练集，在拟合程度过高时给出惩罚。L2正则化是常用的方法，其表达式为$$R(W)=\sum_k\sum_l W_{k,l}^2$$即$W$中每一项的平方求和，在出现某一个权重值非常大时，该值会非常大，也就是，这一项能促进$W$向每一个权重均匀分布的方向优化。

最终的损失函数为$$L=\frac{1}{N}\sum_i L_i+\lambda R(W)$$对Hinge Loss求平均值，$\lambda$是正则化强度，用于控制对过拟合的惩罚力度，是一个hyperparameter

把上面的式子展开，得到$$L = \frac{1}{N} \sum_i \sum_{j \neq y_i} \left[ \max(0, f(x_i; W)_j – f(x_i; W)_{y_i} + \Delta) \right] + \lambda \sum_k \sum_l W_{k,l}^2$$其中$f(x_i;W)=Wx_i,f(x_i;W)_j=w_j^Tx_i$，$x_i$为列向量。

我们的目标就是找到让$L$尽可能小的$W$，可以使用梯度下降法。

随机梯度下降（Stochastic Gradient Descent, SGD）

梯度下降就是求$L$对$W$的偏导数（梯度），然后用它来更新$W$，使$W$朝着减小$L$的方向更新。表达式为$$W_{t+1} = W_t – \eta \cdot \nabla_W L_i(W_t)$$其中$\eta$为学习率，用来控制每一步移动多少，是一个hyperparameter，$\nabla_W L_i(W_t)$就是$L$对$W$中每个元素的偏导数，形状与$W$相同。

随机梯度下降就是每次随机选择一个小样本来计算梯度并更新$W$，对于大数据集更高效。

Softmax

Softmax是一个激活函数，可以把输出的分数转换为概率分布，表达式为$$\sigma(\mathbf{z})_j = \frac{e^{z_j}}{\sum_{k=1}^{C} e^{z_k}}$$$\mathbf{z}$为上面提到的每一类的分数，$z_j$为第$j$类的分数。
可以看出，$\sigma(\mathbf{z})_j \in (0,1) \quad $且$ \quad \sum_{j=1}^{C} \sigma(\mathbf{z})_j = 1$，所以这可以理解成是第$j$类的概率，使用指数的形式，可以把原分数放大，突出某一类别的可能性。

交叉熵损失（Cross-Entropy Loss）

交叉熵损失：待补充

Softmax常与交叉熵损失结合使用，即第$i$组数据损失函数为$$L_i=-log(\frac{e^{s_{y_i}}}{\sum_{j}e^{s_{j}}})$$

令$p_i=\frac{e^{s_{y_i}}}{\sum_{j}e^{s_{j}}}$，并加入L2正则化，总的损失函数$$L=-\frac{1}{N}\sum_i log(p_i)+\lambda R(W)$$我们需要最大化正确类别的概率，即最小化$L$，也可以使用梯度下降法来完成。

梯度计算

待补充